| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 14일 공부
- DevOps
- 회고
- MAPF
- docker
- 논문 정리
- 지표
- 경로 계획 알고리즘
- amazon ecs
- 디자인 패턴
- AWS 비용 절감
- Rust
- leetcode
- study
- terraform
- Go-lang
- Playwright
- 오블완
- ssh
- github
- Til
- PostgreSQL
- 티스토리챌린지
- 커머스
- 생성 패턴
- 구조 패턴
- AWS
- 실용주의 프로그래머
- 신혼 여행
- 청첩장 모임
- Today
- Total
밤 늦게까지 여는 카페
사칙 연산 계산 프로그램 구현하기 feat. Shunting Yard 알고리즘 본문
안녕하세요. 오늘은 사칙 연산을 계산하는 프로그램을 구현하면서 공부한 내용을 정리해보겠습니다.
파이썬으로 구현할 것이고 덧셈, 뺄셈, 곱셈, 나눗셈, 그리고 소괄호를 지원합니다.
처음에는 간단하다고 생각했지만 막상 시작해보니 어렵더라고요;;;
고민한 내용들 간단하게 정리해보겠습니다!
1. 가장 간단한 방법 - eval 🤣
파이썬에는 eval이라는 함수가 있습니다.
주어진 파이썬 코드를 실행할 수 있는 함수라서 사칙 연산도 실행됩니다.

하지만 임의의 파이썬 코드를 실행할 수 있기 때문에 보안적으로 매우 위험합니다 ㄷㄷㄷ
그래서 왠만하면 이렇게 기능을 제공하지는 않습니다 ㅎㅎ
2. 우선 순위 높은 연산들부터 먼저 계산하면 어떨까요?
eval 함수를 사용하지 않고 계산하는 코드를 작성해야 한다면 어떻게 할까요?
트리를 구성해서 연산 순서를 잘 맞출 수 있지 않을까 고민했는데 트리를 어떻게 구성할지부터 막막했습니다.
고민고민하다가 우선 순위 괄호 안의 식들을 모두 계산한 이후에 곱셈, 나눗셈, 덧셈, 뺄셈을 계산하는 방식으로 구현하게 되었습니다.
다음과 같이 간단한 방식입니다.
1. 주어진 문자열 식을 숫자와 부호로 이뤄진 토큰 리스트로 변환합니다.
2. 토큰 리스트를 순회하여 괄호가 없어질 때 까지 다음 작업을 반복합니다.
2.1. 토큰 리스트에서 가장 깊은 괄호 쌍을 찾습니다.
2.2. 2.1에서 찾은 괄호 쌍 내부의 식에서 곱셈, 나눗셈을 계산합니다.
2.3. 2.2에서 계산된 식에서 덧셈, 뺄셈을 계산합니다.
3. 2에서 계산된 괄호가 없는 식에서 곱셈, 나눗셈을 계산합니다.
4. 3에서 계산된 식에서 덧셈, 뺄셈을 계산합니다.
위의 로직을 구현한 코드도 첨부합니다..
from typing import (
Callable,
Dict,
List,
)
def handle_parenthesis(query: List[str]) -> List[str]:
left_stack = []
right_queue = []
for i in range(len(query)):
token = query[i]
if token == "(":
left_stack.append(i)
elif token == ")":
right_queue.append(i)
while len(left_stack) > 0:
l, r = left_stack.pop(), right_queue.pop(0)
evaluated_query = handle_add_and_sub(handle_mul_and_div(query[l+1:r]))
query = query[:l] + evaluated_query + query[r+1:]
right_queue = list(map(lambda x: x-(r-l), right_queue))
return query
def handle_mul_and_div(query: List[str]) -> List[str]:
mul_and_div = {
"*":lambda x, y: str(int(x)*int(y)),
"/":lambda x, y: str(int(x)/int(y)),
}
return _handle_operators(query, mul_and_div)
def handle_add_and_sub(query: List[str]) -> List[str]:
add_and_sub = {
"+":lambda x, y: str(int(x)+int(y)),
"-":lambda x, y: str(int(x)-int(y)),
}
return _handle_operators(query, add_and_sub)
def _handle_operators(query: List[str], operators: Dict[str, Callable]) -> List[str]:
idx = 0
while idx < len(query):
token = query[idx]
if token not in operators:
idx += 1
continue
operand1 = query[idx-1]
try:
operand2 = query[idx+1]
except:
print(query, idx)
raise
operator = operators[token]
query = query[:idx-1] + [operator(operand1, operand2)] + query[idx+2:]
return query
def tokenize_raw_query(raw_query: str) -> List[str]:
result = []
raw_query = raw_query.strip()
for t in raw_query:
if t == ' ':
continue
if t.isdigit():
if len(result) > 0 and result[-1].isdigit():
result[-1] += t
else:
result.append(t)
else:
result.append(t)
return result
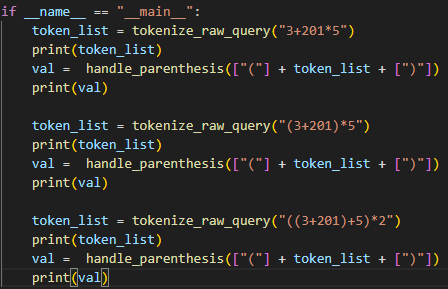
if __name__ == "__main__":
token_list = tokenize_raw_query("3+201*5")
print(token_list)
val = handle_add_and_sub(handle_mul_and_div(handle_parenthesis(token_list)))
print(val)
token_list = tokenize_raw_query("(3+201)*5")
print(token_list)
val = handle_add_and_sub(handle_mul_and_div(handle_parenthesis(token_list)))
print(val)
token_list = tokenize_raw_query("((3+201)+5)*2")
print(token_list)
val = handle_add_and_sub(handle_mul_and_div(handle_parenthesis(token_list)))
print(val)
P.S.
위의 방식을 자세히 보면 2.2, 2.3과 3, 4가 중복되는 것을 확인할 수 있습니다.
실제로 작성된 코드에도 중복 로직이 있는데 어떻게 개선할 수 있을까요?
간단하게도 토큰 리스트의 양 끝에 괄호를 붙여버리면 됩니다!
그러면 제일 바깥 괄호를 처리하면서 식 전체가 계산되어서 중복 로직이 사라지게 됩니다.
1. 주어진 문자열 식을 숫자와 부호로 이뤄진 토큰 리스트로 변환합니다.
2. 1에서 구한 토큰 리스트의 양 끝에 괄호를 붙입니다.
3. 토큰 리스트를 순회하여 괄호가 없어질 때 까지 다음 작업을 반복합니다.
3.1. 토큰 리스트에서 가장 깊은 괄호 쌍을 찾습니다.
3.2. 2.1에서 찾은 괄호 쌍 내부의 식에서 곱셈, 나눗셈을 계산합니다.
3.3. 2.2에서 계산된 식에서 덧셈, 뺄셈을 계산합니다.
3. 후위 표기법으로 바꾼 뒤 실행하는 법 - Shunting Yard 알고리즘
우리가 수식을 작성할 때 일상적으로 사용하는 피연산자 사이에 부호를 쓰는 방식을 중위 표기법이라고 합니다.
중위 표기법은 사람들이 보기에는 굉장히 친화적이지만 컴퓨터 입장에서는 연산의 우선 순위를 파악하기 어려운 구조입니다.
이를 개선하기 위해서 중위 표기법의 우선 순위를 고려하여 후위 표기법으로 바꿀 수 있습니다.
- 중위 표기법: [3, +, 201, *, 5]
- 후위 표기법: [3, 201, 5, *, +]
후위 표기법으로 표현된 식은 계산하기가 매우 간단합니다.
1. 값을 저장하기 위한 스택 S를 생성합니다.
2. 식을 앞에서부터 조회하면서 값을 만나면 1에서 생성한 S에 저장합니다.
3. 부호를 만나면 스택에서 값 2개를 추출해서 연산한 뒤 S에 저장합니다.
4. 식을 전부 돌면 S에 남은 값이 계산의 결과입니다.
그러면 중위 표기법을 후위 표기법으로 바꿔야 하는데 바로 이때 사용되는 것이 Shunting Yard 알고리즘입니다.
Shunting Yard 알고리즘도 단순합니다!
0. 후위 표기법으로 변환된 결과를 저장할 리스트 L과 연산 부호를 저장할 스택 S를 생성합니다.
1. 중위 표기법으로 작성된 식을 순회하면서 다음 작업을 수행합니다.
1.1. 값을 만나면 L에 바로 추가합니다.
1.2. 연산 부호 O를 만나면 S의 마지막 연산 부호의 우선 순위를 확인합니다.
1.3. S의 마지막 연산 부호의 우선 순위가 O의 우선 순위보다 더 높을 시, 추출하고 L에 추가합니다.
1.4. S에 O 를 추가합니다.
2. S에서 연산 부호를 추출하여 L에 추가합니다.
이 로직을 구현한 코드입니다.
from typing import (
Dict,
List,
)
def calculate_postorder(query: List[str]) -> int:
print(query)
operators = {
"+": lambda x, y: x+y,
"-": lambda x, y: x-y,
"*": lambda x, y: x*y,
"/": lambda x, y: x/y,
}
value_stack = []
for token in query:
if type(token) is int:
value_stack.append(token)
else:
operand1, operand2 = value_stack[-2:]
value_stack = value_stack[:-2]
value_stack.append(operators[token](operand1, operand2))
return value_stack[0]
def convert_inorder_to_postorder(query: List[str], operators: Dict[str, int]) -> List[str]:
postorder = []
operator_stack = []
for token in query:
if token in operators:
if len(operator_stack) > 0:
last_operator = operator_stack[-1]
if operators.get(last_operator, -1) > operators[token]:
postorder.append(operator_stack.pop())
operator_stack.append(token)
elif token == "(":
operator_stack.append(token)
elif token == ")":
while True:
operator = operator_stack.pop()
if operator == "(":
break
postorder.append(operator)
else:
postorder.append(token)
postorder += operator_stack[::-1]
return postorder
def tokenize_raw_query(raw_query: str) -> List[str]:
result = []
raw_query = raw_query.strip()
for t in raw_query:
if t == ' ':
continue
if t.isdigit():
if len(result) > 0 and result[-1].isdigit():
result[-1] += t
else:
result.append(t)
else:
result.append(t)
for i in range(len(result)):
if not result[i].isdecimal():
continue
result[i] = int(result[i])
return result
if __name__ == "__main__":
operators = {
"+":0,
"-":0,
"*":1,
"/":1,
}
token_list = tokenize_raw_query("3+201*5")
val = calculate_postorder(convert_inorder_to_postorder(token_list, operators))
print(val)
token_list = tokenize_raw_query("(3+201)*5")
val = calculate_postorder(convert_inorder_to_postorder(token_list, operators))
print(val)
token_list = tokenize_raw_query("((3+201)+5)*2")
val = calculate_postorder(convert_inorder_to_postorder(token_list, operators))
print(val)
식을 계산하는데 훨씬 효율적인 방법이 있었네요...!
'알고리즘 > 문제풀이' 카테고리의 다른 글
| [leetcode] 399. Evaluate Division - 이번에도 Runtime 100%! (0) | 2025.06.03 |
|---|---|
| [leetcode] 75. Sort Colors - 이번에는 Runtime 100% 찍었습니다! (0) | 2025.05.20 |
| [leetcode] 2257. Count Unguarded Cells in the Grid #3 (2) | 2024.11.29 |
| [leetcode] 2257. Count Unguarded Cells in the Grid #2 (1) | 2024.11.27 |
| [leetcode] 2257. Count Unguarded Cells in the Grid (1) | 2024.11.23 |




