반응형
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- study
- 실용주의 프로그래머
- 경로 계획 알고리즘
- 논문 정리
- AWS 비용 절감
- leetcode
- ssh
- 디자인 패턴
- Go-lang
- 구조 패턴
- MAPF
- 신혼 여행
- 오블완
- Rust
- DevOps
- Til
- 도커 주의사항
- AWS
- PostgreSQL
- 생성 패턴
- Monthly Checklist
- Playwright
- github
- amazon ecs
- terraform
- 청첩장 모임
- 티스토리챌린지
- 지표
- 14일 공부
- docker
Archives
- Today
- Total
밤 늦게까지 여는 카페
IDA* 알고리즘 - A* 변형은 끝이 없는 것 같습니다. 본문
안녕하세요. 오늘은 A* 알고리즘의 변형 중 하나인 Iterative Deepning A*(IDA*) 알고리즘을 공부해보려고 해요!
- Stuart Russell. 1992. Efficient memory-bounded search methods. In Proceedings of the 10th European conference on Artificial intelligence (ECAI '92). John Wiley & Sons, Inc., USA, 1–5.
저번에 SMA* 알고리즘을 공부했던 논문에서 IDA* 알고리즘을 봐버려서 넘길수가 없었습니다...
IDA* 알고리즘을 간단하게 설명하면 탐색 깊이를 제한함으로써 메모리를 아끼는 것인데요.
자세히 알아보도록 하겠습니다.
1. IDA* 알고리즘 동작 방식
- 시작 노드 s의 f ` 값을 계산합니다.
- 노드 s의 f` 값을 LIMIT에 대입합니다.
- 노드 s에 대해서 LIMIT값과 함께 DFS 알고리즘을 실행합니다.
- DFS 알고리즘의 반환값에 SUCCESS가 있다면 알고리즘을 종료합니다..
- DFS 알고리즘의 반환값이 FAILED라면 같이 반환된 f`값을 LIMIT으로 갱신합니다.
- 3로 돌아갑니다.
DFS 알고리즘
- 주어진 노드 n의 f` 값이 LIMIT 값보다 크다면 (FAILED, f`(n)) 을 반환합니다.
- 만약 노드 n이 goal 노드라면 (SUCCESS, -) 을 반환합니다.
- Connected(n)에 포함된 c들에 대해서 DFS(c, LIMIT)을 실행하고, 가장 작은 f` 값을 반환합니다.
동작 방식을 보면 IDA* 알고리즘이 대략적으로 어떻게 동작하는지 아시겠죠?
이제 최단 경로를 찾을 수 있도록 조금 더 구체적인 예제 코드를 준비하겠습니다.
2. 예제 코드
from dataclasses import dataclass
from typing import List
@dataclass
class Node:
id: int
is_visited: bool = False
f_val: float = float("inf")
parent_id: int = None
@dataclass
class Edge:
start_node: Node
end_node: Node
weight: float
def get_weight(self) -> float:
return self.weight
def get_other_node(self, node_id: int) -> Node:
if self.start_node.id == node_id:
return self.end_node
else:
return self.start_node
@dataclass
class Graph:
nodes: dict
adjacent_edges: dict
def get_node(self, node_id: int) -> Node:
return self.nodes[node_id]
def get_node_f_val(self, node_id: int) -> int:
return self.nodes[node_id].f_val
def set_node_f_val(self, node_id: int, f_val: int):
self.nodes[node_id].f_val = f_val
def get_adjacent_edges(self, node_id: int) -> List[Edge]:
return self.adjacent_edges.get(node_id, [])
def trace(self, node_id):
parent_id = self.nodes[node_id].parent_id
if parent_id != None:
return self.trace(parent_id)+ [node_id]
return [node_id]
def ida(graph, start_node_id, end_node_id):
success = False
limit = 0
graph.set_node_f_val(start_node_id, 0)
while True:
old_limit = limit
visited = {start_node_id:0}
(success, f_val) = dfs(graph, start_node_id, end_node_id, limit, visited)
if success:
return graph.trace(end_node_id)
limit = f_val
if limit == old_limit:
return "Failed to find path"
def dfs(graph, node_id, goal_node_id, limit, visited):
f_val = graph.get_node_f_val(node_id)
if f_val > limit:
return (False, f_val)
if node_id == goal_node_id:
return (True, f_val)
result = []
for connected_edge in graph.get_adjacent_edges(node_id):
connected_node = connected_edge.get_other_node(node_id)
if not connected_node.is_visited or connected_node.f_val > f_val + connected_edge.weight:
connected_node.is_visited = True
connected_node.parent_id = node_id
graph.set_node_f_val(connected_node.id, f_val + connected_edge.weight)
r = dfs(graph, connected_node.id, goal_node_id, limit, visited)
result.append(r)
result = sorted(result, key=lambda x:(x[0]==False, x[1]))
try:
return result[0]
except:
return (False, float("inf"))
if __name__ == "__main__":
if __name__ == "__main__":
nodes = {}
for i in range(11):
nodes[i+1] = Node(id=i+1)
adjacent_edges = {}
adjacent_edges[1] = [Edge(start_node=nodes[1], end_node=nodes[2], weight=1)]
adjacent_edges[1] += [Edge(start_node=nodes[1], end_node=nodes[3], weight=2)]
adjacent_edges[1] += [Edge(start_node=nodes[1], end_node=nodes[4], weight=1)]
adjacent_edges[2] = [Edge(start_node=nodes[2], end_node=nodes[6], weight=1)]
adjacent_edges[2] += [Edge(start_node=nodes[2], end_node=nodes[11], weight=1)]
adjacent_edges[3] = [Edge(start_node=nodes[3], end_node=nodes[5], weight=1)]
adjacent_edges[3] += [Edge(start_node=nodes[3], end_node=nodes[6], weight=4)]
adjacent_edges[3] += [Edge(start_node=nodes[3], end_node=nodes[8], weight=3)]
adjacent_edges[5] = [Edge(start_node=nodes[5], end_node=nodes[7], weight=2)]
adjacent_edges[5] += [Edge(start_node=nodes[5], end_node=nodes[8], weight=1)]
adjacent_edges[7] = [Edge(start_node=nodes[7], end_node=nodes[9], weight=1)]
adjacent_edges[8] = [Edge(start_node=nodes[8], end_node=nodes[10], weight=1)]
adjacent_edges[9] = [Edge(start_node=nodes[9], end_node=nodes[10], weight=1)]
adjacent_edges[11] = [Edge(start_node=nodes[11], end_node=nodes[8], weight=1)]
graph = Graph(nodes=nodes, adjacent_edges=adjacent_edges)
print(ida(graph, 1, 10))3. 예시
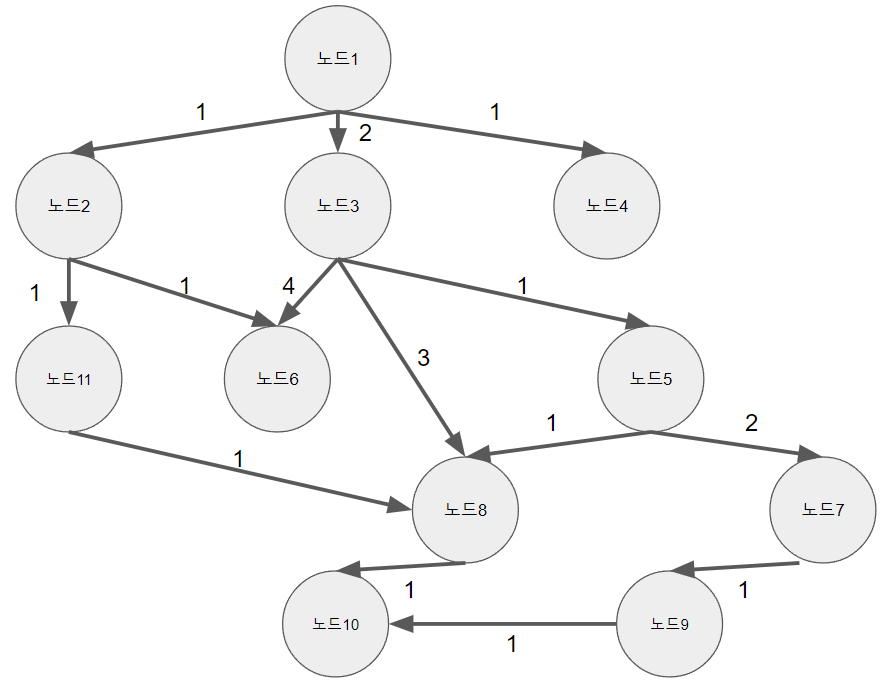
실행 결과
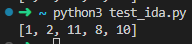
IDA*알고리즘은 어떠셨나요?
저는 IDA* 알고리즘이 SMA* 알고리즘보다 훨씬 직관적이고, 구현이 쉽더라구요!
SMA* 알고리즘 예제 코드는 언제 준비할 수 있을지...
읽어야 할 논문이 너무 많습니닷...
요즘 일이 바빴는데 여유가 생기면 꼭 마무리 하도록 하겠습니다!
다들 바쁘시겠지만 화이팅입니다!
반응형
'알고리즘 > Path Finding' 카테고리의 다른 글
| WA* 알고리즘 - Heuristic 함수에 장난을 좀 쳐볼까요? (0) | 2023.05.05 |
|---|---|
| PEA* 알고리즘 - 이렇게 간단하다구요? 그럼에도 메모리 효율적이라구요? (0) | 2023.04.30 |
| SMA* 알고리즘 - 메모리를 고려한 A* 알고리즘의 변형이 또 있네요! (0) | 2023.04.14 |
| 한눈에 보는 경로 계획 알고리즘 공부 순서 (5) | 2023.04.08 |
| RBFS 알고리즘 - A* 알고리즘이 메모리를 너무 많이 사용할 때는 어떻게 해야 할까요? (0) | 2023.04.08 |



